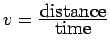
Diameter=![]() Circumference=2
Circumference=2![]()
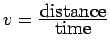
![]() angular diameter
angular diameter
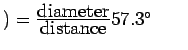 distance (pc)=
distance (pc)=
![]()
![]()
![]()
![]()
![]() In solar units:
In solar units:
![]()
Brightness
![]() (
(![]() )
)
![]()
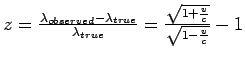
![]()
perihelion=
![]() aphelion=
aphelion=
![]()
![]()
![]()
![]()
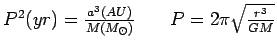
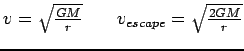 fraction remaining
fraction remaining
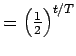
Condition for escape:
![]()

![]() km/s
km/s
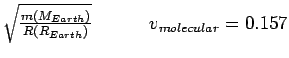 km/s
km/s
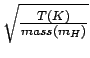
![]()
![]()
![]()
![]() age
age
![]() billion yrs
billion yrs