3 Rides

In this section we will discuss how you can apply physics principles to some of the rides at the South Carolina State Fair. Analyze several of the rides mentioned in this booklet yourself and then use those rides as starting places for investigating other rides.

One of the measurable aspects of fair rides is the force that they exert on you and the acceleration you experience. The force and acceleration are connected through Newton’s second law; F = ma, where F is the force in units of Newtons (N), m is the mass in kilograms (kg), and a is the acceleration in meters per second squared (m/s2). Remember, it is the force that causes the acceleration, not the other way round. That is, F = a/m.

When the only force on you is the force of gravity, your weight is W = mg, where g is the acceleration of gravity (9.81 m/s2). When you feel “pushed down” at the bottom of a roller-coaster loop, you experience an apparent weight greater than your normal weight. If your apparent weight is twice your normal weight, we say that you are experiencing a force of “two gs.” That is because the force needed to accelerate you in the proper direction exceeds your normal weight and must be supplied by the ride. At the top of a roller-coaster hill you may feel yourself being lifted from your seat. That is because the coaster is being accelerated downward faster than g and the restraining lap bar is needed to give you the acceleration needed to keep up with the car. One of the objects of ride physics is to measure and calculate the acceleration of a rider.

3.1 Roller Coasters; Non-looping and Looping, Clothoids

A roller coaster provides a good example of conservation of energy. The train is pulled to the top of a high hill and let go (Fig. B1). The train then plunges down the other side of the hill. It then rises up another hill to plunge down again, perhaps with twists and turns to the left and right.

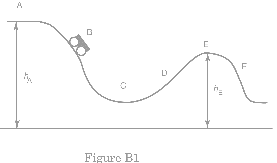
We can understand the motion of a roller coaster by considering conservation of mechanical energy. Assume the car is hauled up to point A in the figure. At point A the total mechanical energy is equal to the total mechanical energy at point E, as it is at all of the points on the track. (For the purpose of getting a general understanding, we are omitting the energy converted into heat by friction. You may want to try to estimate the magnitude of frictional effects in a more refined analysis. However you can best understand things by leaving frictional effects out at the beginning.) Thus the sum of the potential energy (PE) and kinetic energy (KE) is the same at points A and E.

Therefore we can calculate the speed at E if we know the heights hA and hE. If the train is moving slowly at the top of the first hill (A) we can neglect the term to find

To make the ride more exciting the roller coaster designers may put a loop – or even two loops – in the track, as shown in Fig. B2. They must choose the maximum height of the loop, and also the shape of the loop.

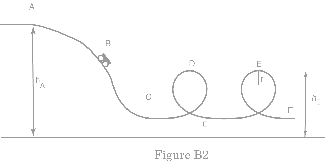
You can estimate the maximum height of the loop, or to turn the question around, can you estimate what fraction of the initial potential energy at A is lost to friction if the car has a given speed at position E and height hE.

If the loops were circular, the riders would experience 6 gs at the bottom and would just barely hang on (0 gs) at the top of the loop. This is under the assumption that the coaster enters the loop at a given speed at C and is slowed by the force of gravity as it coasts up to the top of the loop at D. Humans can not tolerate 6 g's in this situation so another shape rather than a circle is used for the loop.

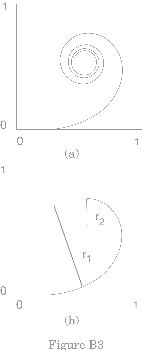
The shape normally used is part of a spiral called a clothoid. A clothoid spiral is useful for joining trajectories and is sometimes used in highway and railroad interchanges. The radius of curvature of a clothoid varies linearly with the arc length, starting at the origin, and the center of curvature is not a fixed point, but depends on where you are on the curve (Fig. B3b). Thus when entering the loop at a given speed v your centripetal acceleration v2/r need not be too large. However, when you have reached the top of the loop, with a lower speed v,the radius of curvature has decreased so that v2/r will be large enough so that the net force will hold you in your seat.

3.2 Rotating Rides and Swings

Merry-Go-Round

Perhaps the simplest rotating ride is a merry-go-round. You can make interesting measurements on it. Fig. B4 is a schematic diagram of a merry-go-round with two rows of horses. Here we will not include the up-and-down motion of the horses, so make your measurements standing on the rotating platform. The horizontal component of the centripetal acceleration of is ac = v2/r for a horse at a distance r from the axis of rotation and moving at a linear (tangential) speed v.

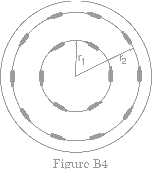
In terms of the period T, the time for one complete rotation, we can write

Because the period T is the same for all horses, no matter what their distance from the axis, we can write the ratio of the centripetal acceleration at two different distances r1 and r2 as

You should determine r1 and r2 and measure ac(1) and ac(2) with your horizontal accelerometer and see how your measurements compare with the formula above.

Rotator (Starship 2000)

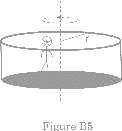
Another simple ride is sometimes called Rotator.(Fig.B 5) Riders stand with their backs against the wall in a cylindrical chamber that can be rotated about its vertical central axis. When the ride has reached a certain speed the floor drops down and the riders are held against the wall by frictional forces. Can you estimate the minimum coefficient of friction between the riders and the wall needed to keep them from falling?

Round Up

Other rides begin rotating in a horizontal plane and then tip up until the axis of rotation is almost horizontal. In these rides the riders may stand against a wall, as in the Round Up or they may be in cars or cages, as in the Enterprise. Taking the Round Up as an example (Fig. B.6), note that in the horizontal position the acceleration -or force- is just that of the Rotator. As the circling

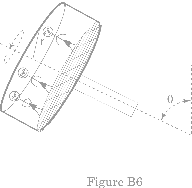
ride is tipped up the force changes as you go around because the force exerted on you due to the ride is always toward the center of rotation but the force of gravity is always downward. We can write

where F is the net force acting on you while riding the Round Up, Fwall is the towards-the-center force exerted on you by the wall of the Round Up, and Fgravity is the force of gravity acting on you (toward the center when at the top of the ride and away from the center at the bottom of the ride). If the Round Up were tilted over until it rotates in a vertical plane then the net force acting on you the rider when you were at the top of the ride would be

F = Fwall + Fgravity.

In that case, the force of the wall on you can be expressed as

Fwall = F – Fgravity.

The force due to the wall is reduced because gravity is helping to accelerate you. In terms of acceleration, the last equation becomes

Similarly, at the bottom of the ride, the wall force must increase because the directions are changed. Thus at the bottom the acceleration is given by

To be more precise we note that the Round-Up is tilted up to a steep angle, but less than 90°,
(q < 90°). When the angle between the plane of the rotating platform and vertical plane is q, the result is that the acceleration along the radial direction becomes

where the minus sign is for the top and the plus sign is for the bottom.

Swings

When a rotating swing has a vertical axis as shown in Fig. B7 the angle q at which the swingers ride is given by the formula below where R is the distance from the axis of rotation and T is the time for one revolution.

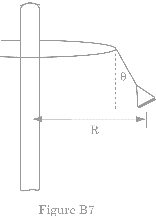
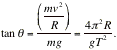
What does this formula predict about the angles of the riders compared to the angles of the riderless swings? Notice that there are two rows of swings and riders. Why don’t the swings collide? How does the behavior change for the Wave Swinger, which has a tilted axis of rotation?

3.3 Compound Motion Rides

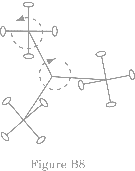
The motion of some rides is so complicated that it is unrealistic to try to derive a formula that gives, say, the acceleration as a function of time. Figure B8 is a schematic of a ride called the Scrambler. Each car moves in a circle about an axis which itself moves in a circle. On some rides there also may be up-and-down motion or in-and-out motion. Observe the rides and make a rough sketch. Determine where the maximum change in velocity will occur and check your predictions by making measurements with your accelerometer. Estimate the maximum speed assuming that the carts go from a stop to a maximum and back to a stop as they swing from one side to the other. Approximate the motion as linear and the acceleration as constant over each half of the path.

3.4 Drops

There are at least two types of “drops.” One is similar to a parachute ride and the other is close to a free-fall. For either case you should be able to think of some measurements and observations. The parachute type has been around for some time and the free-fall type (Drop of Fear) is now being brought to the fair. The rider is dropped from the top of a tall tower between rails that are nearly friction free. You should measure the height of the fall and then calculate the speed at the bottom. You can also calculate the expected time for a friction-free fall. Then measure the final speed or time-of-fall and comment on how friction-free the ride is. If you have a CBL-system, measure the acceleration in the vertical direction as you fall as well as the air pressure. The air pressure data can later be used to measure your vertical position.

3.5 Ride Data

Here we have listed some, but not all, of the parameters of several rides. You will need to make some measurements for yourself.

G – FORCE

This is a relatively new ride at the South Carolina State Fair
The claim is that it gives 4 gs. (What do you measure?)
Platform, 4 rpm.
Beam, 5 rpm.
Carousel, 0 to 17 rpm no quicker than 15 seconds.
Break time, 17 to 0 rpm no quicker than 9 seconds.

DOPPLE LOOP
Double looping roller coaster.
Height of first drop: 104 ft.
Height of loop: 45 ft.

ENTERPRISE
Tilting circular ride.
Diameter of wheel: 55 ft.
Rotation speed: 13.5 rpm.
Angle with the horizontal: maximum 87°.

POLAR EXPRESS OR THE HIMALAYA
Tilted compound motion.
Radius of the ride: 20 feet
Rotation speed: 4.8 seconds per revolution
Height gain to highest point of ride: 9 feet

GIANT WHEEL
A Ferris wheel
Radius: 52 ft.

ROUND UP
Tilted circular ride.
Radius of ride: 15 ft.
Rotation speed: 16 rpm
Angle with the horizontal: varies.

RAINBOW
A rotating horizontal platform.
Speed: 9-9.5 revolutions per minute
Length of arm: 30 ft.

WAVE SWINGER
Rotating swings.
Length of chain: 16 feet, 6 inches
Radius of rotation: 37 feet, 2 inches
Speed: 6 seconds for one revolution

WILD CAT
Corkscrew roller coaster.
Length of track: 560 m
Time for ride: 95 seconds
Length of car: 7 feet, 9 inches
Weight of car: 800 lb, holds 4 people
Length of first drop: 77 feet
Time for the first drop: 2 seconds
Height of the first hill: 46 feet
Radius of the first curve: 27 feet, 2 inches