HW 2 - due 2 February 2006
SCCC 116
Review and Discussion section: 18-18, 19-11, 20-4
In the Problem section: 19-3, 20-4
Prof. Christina Lacey

R&D 18-18

If our Sun were surrounded by a cloud of gas, would the cloud be an emission nebula?

Our Sun would not produce much of an emission nebula because it emits very little ultraviolet (UV) light. What little UV light emitted by our Sun, would be quickly absorbed by the gas nearest the Sun and the inner emission nebula would be hidden by the glare of sunlight.

R&D 19-11

Stars live much longer than we do, so how do astronomers test the accuracy of theories of star formation?

Astronomers create computer models in which simulations of stellar evolution take weeks instead of millions of years. Astronomers also observe many stars, which are in different stages of formation and evolution and compare these to those predicted by the computer models. The observations are then used to further refine the computer models.

R&D 20-4

Without the fusion of hydrogen into helium occurring in the core, the core no longer has an energy source. Gravity is then able to collapse the core, hydrogen fusion continues in a shell around the core for about another billion years.

P 19-3

For Stage 4:
$T_{stage~4}=3000K=3000K\frac{1 T_{\odot}}{5800K}=0.52 T_{\odot}\\ R_{stage~4}=2\times10^8~km\frac{R_{\odot}}{7\times10^5~ km}=290 R_{\odot}$

In solar units: $L=R^2T^4$
$L=(290 R_{\odot})^2(0.52 T_{\odot})^4=82,000\times 0.072=5900~L_{\odot}$

For Stage 6:
$T_{stage~6}=4500K=4500K\frac{1 T_{\odot}}{5800K}=.78 T_{\odot}\\ R_{stage~6}=1\times10^6~km=1\times10^6~km\frac{R_{\odot}}{7\times10^5~ km}=1.4 R_{\odot}$

In solar units: $L=R^2T^4$
$L=(1.4 R_{\odot})^2(0.78 T_{\odot})^4=1.96\times 0.37=.72~L_{\odot}$

Ratio of luminosity: $\frac{5900~L_{\odot}}{.72~L_{\odot}}=8100$
so the luminosity has decreased by 8100 times (the book gets 7900, the difference is caused by rounding the numbers)

Difference in absolute magnitude, M:

$M=4.85-\log{L(L_{\odot})}$
$M_{stage~4}=4.85-2.5\log{5900}=4.85-2.5(3.8)=-4.65$
$M_{stage~6}=4.85-2.5\log{.72}=4.85-2.5(-1.4)=4.85+.36=5.2$

$M_{stage~6}-M_{stage~4}=5.2-(-4.65)=9.9$
So the difference in absolute magnitudes is 9.9.

------

If you are comfortable with logarithms, then one can just use the ratio:

$\frac{L_{stage~6}}{L_{stage~4}}=\frac{R_{stage~6}^2}{R_{stage~4}^2}\frac{T_{stage~6}^4}{T_{stage~4}^4}$

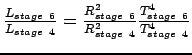
$\frac{L_{stage~6}}{L_{stage~4}}=(\frac{1\times10^6~km}{2\times10^8~km})^2(\frac{4500K}{3000K})^4$=0.00127

So: $\frac{L_{stage~4}}{L_{stage~6}}=\frac{1}{0.00127}=7900$

$M_{stage~6}-M_{stage~4}=4.85-2.5\log{L_{stage~6}} - (4.85-2.5\log{L_{stage~4}})$
$=-2.5\log{L_{stage~6}} + 2.5\log{L_{stage~4}}$
$=2.5(\log{L_{stage~4}}-\log{L_{stage~6}})$
$=2.5\log{\frac{L_{stage~4}}{L_{stage~6}}}=2.5\log(7900)=2.5(3.9)=9.7$
$M_{stage~6}-M_{stage~4}=9.7$

(the difference in magnitudes is positive, so stage 6 is dimmer than stage 4)

P 20-4
Calculate the radius of a 12,000 K (2$~T_\odot$), 0.0004 L$_\odot$ white dwarf.

$R=\frac{\sqrt{L}}{T^2}$ in solar units.

$R=\frac{\sqrt{0.0004}}{2^2} =0.005~R_\odot\frac{7\times 10^5~km}{1~ R_\odot}$=3500 km