Question 1: Q: How many miles and m are in a light year?
A: Distance traveled is: ![]() , where v= velocity and t is the
time traveled. For light,
, where v= velocity and t is the
time traveled. For light, ![]() =speed of light=
=speed of light=![]() and
and ![]() 1 year.
1 year.
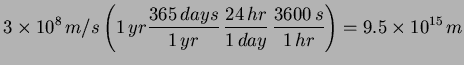 |
|||
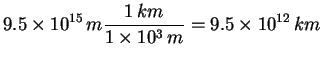 |
|||
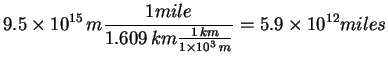 |
P 1-2
a) Write the following in scientific notation:
| (1) |
| (2) |
P 1-6
Through how many degrees, arcminutes, or arcseconds does the moon move in:
a) 1 hour of time
The moon takes 29.5 days to revolve around the Earth once:
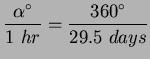 |
|||
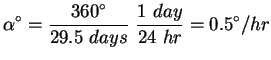 |
(3) |
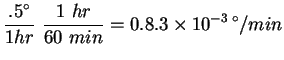 |
|||
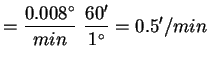 |
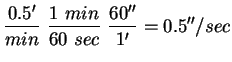 |
(4) |
P 1-9
At what distance is an object if its parallax, as measured from either
end of a 1000 km baseline is:
a) parallax=1![]()
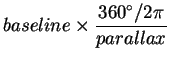 |
|||
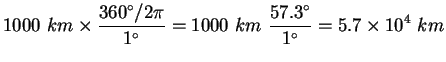 |
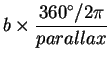 |
|||
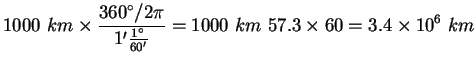 |
(5) |
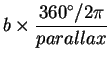 |
|||
 |
(6) |
P 1-11
Calculate the parallax, using Earth's diameter as a baseline, of the Sun's nearest neighbor, Proxima Centauri, which lies 4.3 l.y. from Earth.
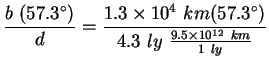 |
|||
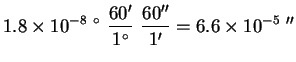 |
(7) |
P 1-13
The moon lies roughly 384,000 km from Earth and the Sun lies about
150,000,000 km away. If both have the same angular size as seen from
Earth, how many times larger is the Sun than the moon?
Let ![]() =diameter and
=diameter and ![]() distance:
distance:
| (8) |
 |
 |
 |
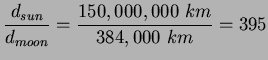 |
(11) |
P 2-9
Jupiter's moon Callisto orbits Jupiter at a distance of 1.88 million
km (
![]() km). Callisto's orbital period about Jupiter is
16.7 days (=P). (Assume Callisto's mass is negligible compared to
Jupiter). What is the mass of Jupiter?
km). Callisto's orbital period about Jupiter is
16.7 days (=P). (Assume Callisto's mass is negligible compared to
Jupiter). What is the mass of Jupiter?
From Eq. 2.7 in textbook:
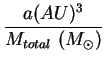 |
|||
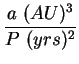 |
(12) |
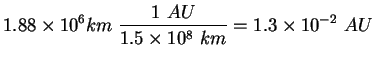 |
|||
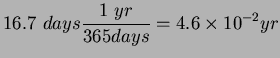 |
|||
| (13) |
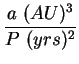 |
|||
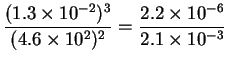 |
|||
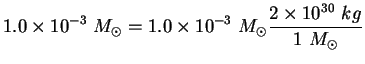 |
|||
| (14) |
P 2-15
The Moon's mass is
![]() kg and the radius of the
Moon is
kg and the radius of the
Moon is ![]() km. What is the speed of a spacecraft moving
in a circular orbit just above the lunar surface? What is the escape
speed?
km. What is the speed of a spacecraft moving
in a circular orbit just above the lunar surface? What is the escape
speed?
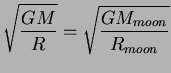 |
|||
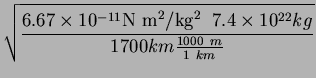 |
|||
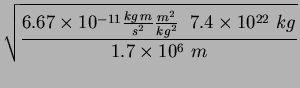 |
|||
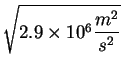 |
|||
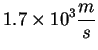 |
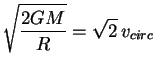 |
|||
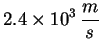 |
(15) |